How to model the hardest materials in the universe? | Urania

The hardest materials in the universe are not graphene, spider webs, or diamonds. It is the crystalline shell of a neutron star. If a teaspoon of it were dropped to the surface of the Earth, it would weigh about 5 tons. In the latest paper, astronomers modified fluid dynamics models to simulate this exotic material.

There has been a popular scientific debate about this topic One of the most read news in 2023 On the American Astronomical Society AAS Nova website.

Unparalleled material

Almost all of the visible matter in our universe is in the form of plasma, which astrophysicists are racing to simulate using fluid dynamics models. Solids often require a different approach when modeling because they have a property called… to bearWhich does not contain plasma. These are resistant to cracking or deformation. The strength of matter is an important feature of a neutron star's shell, which consists of ions that form a crystal lattice. The shell of a neutron star is the hardest matter in the universe. A teaspoon of this strange substance would weigh about 5 tons if it were brought to the surface of the Earth.

This unusual stiffness means that the neutron star's crust cannot be simulated using typical fluid dynamics models, which do not take into account the strength of the material.
In the latest publication by a team of astrophysicists led by Irina Sagert (Los Alamos National Laboratory) addressed this problem of modeling the shell of a neutron star using fluid dynamics models

​

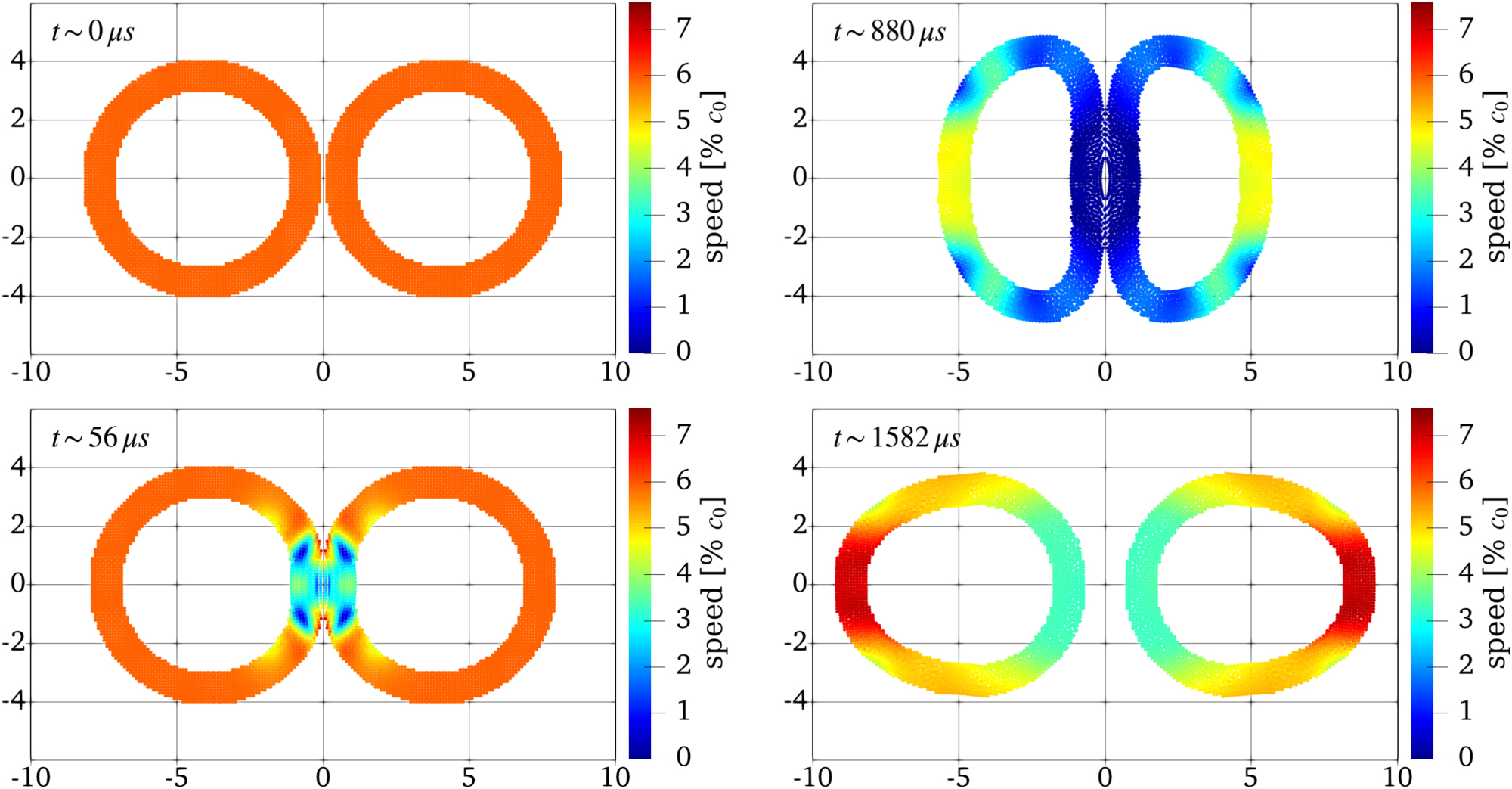
In the illustration: Snapshots at time t (microseconds) of the rubber rings collision. The color indicates the percentage of sound speed of the simulated particles. Source (CC BY 4.0): I. Sagert et al. 2023 ApJS 267 47

Create a solid body model

The team, led by Saggert, took advantage of the opportunity Hydrodynamics of smooth SPH molecules (Smooth Particle Hydrodynamics) in a model called FleCSPH to simulate waves in the shell of a neutron star. It is thought that these waves can explain certain properties of X-ray bursts in neutron stars and influence the gravitational waves generated when neutron stars approach each other on a collision course. Previous simulations of the behavior of neutron stars using smooth particle hydrodynamics (SPH) treated these stars entirely as liquid – including their crust. Therefore, it was impossible to study these waves. Saggert and colleagues' model includes a solid shell surrounding a liquid core.

Before using this model to simulate neutron stars, tests were performed for several of the following configurations:
• Two colliding rubber rings compress and bounce against each other.
• A spherical metal projectile that explodes (i.e. collapses inward).
• A cylindrical metal rod collides with a solid surface.
Although these scenarios seem far from the simulation of the neutron star shell mentioned above, the tests show the ability of this model to realistically reflect the behavior of a solid body under various influences. Pressures. This model has passed all the above tests. Tests – which allowed astrophysicists to apply them to the main mission.

​

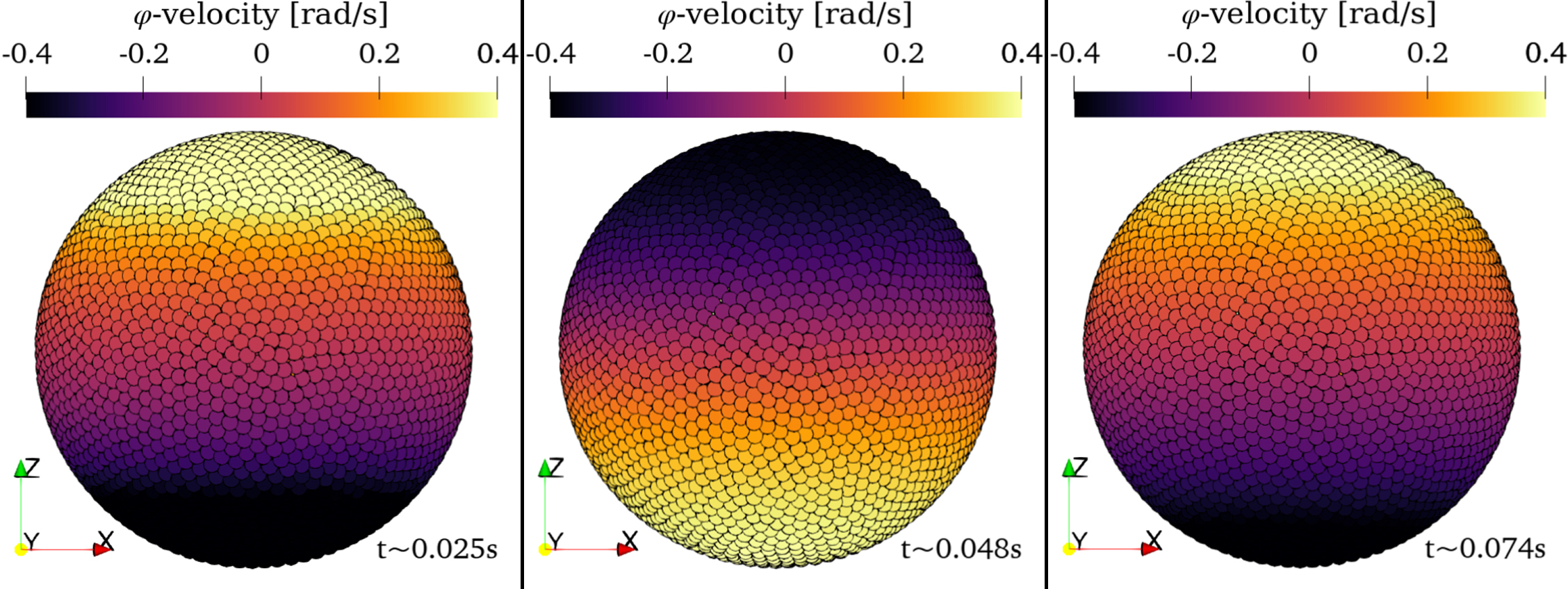
In the illustration: A model of the annular oscillations of a neutron star's crust. Source (CC BY 4.0): I. Sagert et al. 2023 ApJS 267 47

Challenges and future trends

The team of astrophysicists applied their model to simulate propagation Toroidal Waves in a solid-shell neutron star. Scientists faced several challenges in doing this:
• The shell is only a small fraction of the total volume of the neutron star, so all the computing power goes into simulating the liquid core rather than the shell itself.
• In the simplest case, when a neutron star has no magnetic field, there should be no friction between the crust and the core. However, given how calculations are done in the smooth particle (SPH) model, there will always be some friction between the shell and the neutron star core in the simulations.
• Despite its extreme density and rigidity, the shell of a neutron star has something in common with gelatin – it is more resistant to pressure from all directions than to rupture. This property means that small numerical fluctuations in the density of this crust can grow into large fluctuations until they are damped.

Astrophysicists have discovered several ways to deal with the above. Challenges and results of numerical simulations in this model show promising agreement with analytical models.
The search for models of the neutron star's crust is far from over, but Saggert and his colleagues see more opportunities to improve them. When relativistic physics is incorporated into the model, a new window opens for accurately modeling neutron star mergers. This will allow astrophysicists to study neutron star collisions and massive X-ray flares generated by cracks in their crust much more precisely than before.

Prepared by: Ryszard Pernikovich

more information:

• (Scientific publishing) → Modeling solids in nuclear astrophysics using smooth particle hydrodynamics
• How to model the strongest matter in the universe
• A look back at astronomy in 2023 with AAS Nova
•
• Urania Gate: → “Mountains” on neutron stars – if they exist – must generate gravitational waves
• Microscopic deformation of a pulsar as a source of gravitational waves
• Speed ​​record on a neutron star

Source: AAS Nova

In the illustration: An artistic vision of a neutron star formed after the collapse of the nucleus of a massive star and the star's explosion in the form of a supernova. source: He is one. sidewalk